Controls

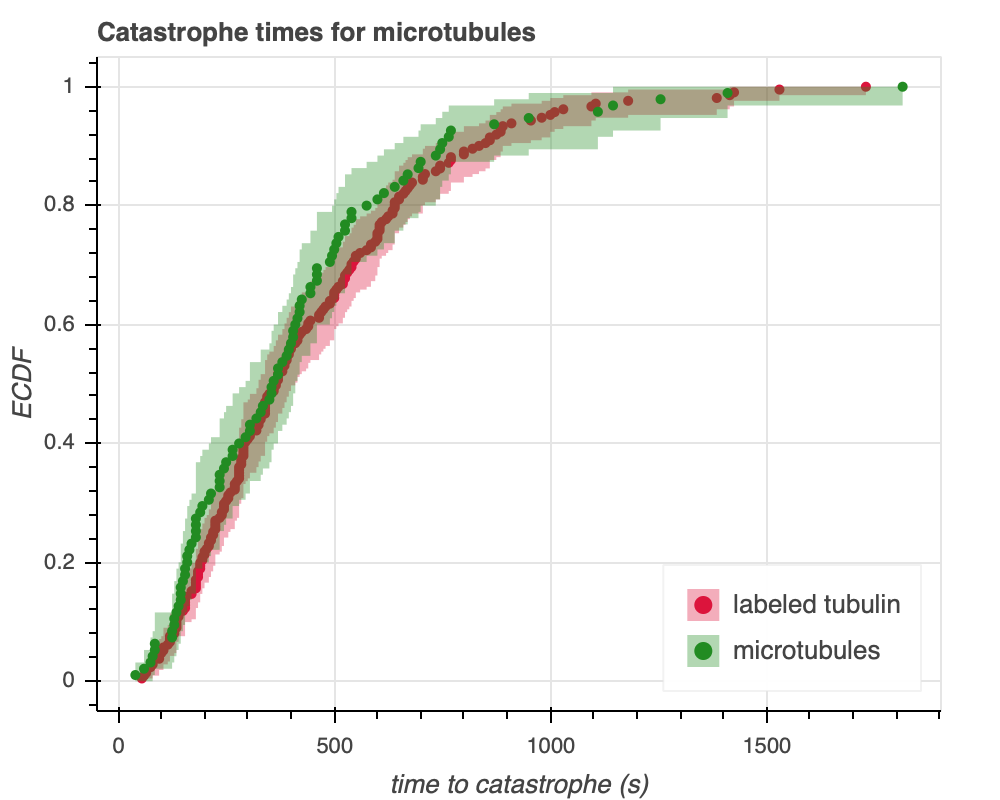
Gardner et al. monitored fluorescently labeled tubulin to measure catastrophe times. As a control to ensure that the fluorescent labels did not interfere with tubulin dynamics, they performed a positive control experiment where they compared labeled and unlabeled microtubule catastrophe times. For the unlabeled tubulin, the catastrophe time was determined using differential interference contrast (DIC) microscopy. Let's compare the catastrophe time distributions for these two groups. Figure 1a shows an empirical cumulative density function (ECDF) of the two distributions, with $95$% confidence intervals based on bootstrapping.

Figure 1a script dataset

We see that the confidence intervals between the labeled and unlabeled tubulin overlap by quite a bit, so they could indeed be identically distributed. In particular, the median values between the two groups overlap, and the confidence interval for the labeled tubulin appears to lie entirely within the confidence interval for the unlabeled group.

Since the intervals don't overlap at all points, however, we can investigate further by doing some statistical tests. We'll compare the difference of the means to get a better sense for how these distributions might be fundamentally different or identical. Since we are assuming (as our null hypothesis) that the two distributions are identically distributed, the mean is as good a statistic as any other, since it captures an overall idea of every single data point. We also considered using the median, but since we aren't making any assumptions about the distribution (i.e. this is non-parametric, rather than parametric inference), there is no reason to pick the median over the mean. In fact, the mean might be better than median––for means, the value of every point is directly considered, rather than indirectly considered through rank as is the case for medians. To look at our chosen test statistic, we used the controls.py module. Here, the data points are shuffled to simulate the null hypothesis that the distributions of microtubules and labeled tubulin are the same. Unlike bootstrap replicates, the data points are drawn without replacement. We get that the difference of means is $28.185$ seconds, with the labeled tubulin taking longer to undergo catastrophe. We get a p-value of $0.224$. Following the standard of using $\alpha = .05$, a p-value of $0.23$ fails to reject the null hypothesis that these distributions are the same. The difference of means that was observed experimentally was $28$ seconds, while our null hypothesis hypothesizes that it should be $0$ seconds. Thus, the probability of observing a difference of means at least as extreme as $28$ seconds when the datasets are the same is around $.22$, so it is not statistically "significant."

We can also look at the studentized difference of means to see what we get there. This metric takes into account the standard deviation, which has the potential to be helpful given that our sample sizes differ but are both relatively small. Again using the controls.py module, we get the experimental studentized difference of means is 0.752 seconds and the p-value is 0.230. There's still only a $23.4$% chance that the means are this different while the generative distributions are the same, but there's a pretty good chance that the mean for labeled tubulin is a bit slower. That said, the medians looked a lot more similar. Based on the ECDF plots, it looks like the labeled tubulin had more catastrophe times above $1000$ seconds, which explains why the mean value is higher. The bulk of tubulins could be about the same, but it seems like labeling the tubulin could encourage some of them to catastrophize at a slower rate.

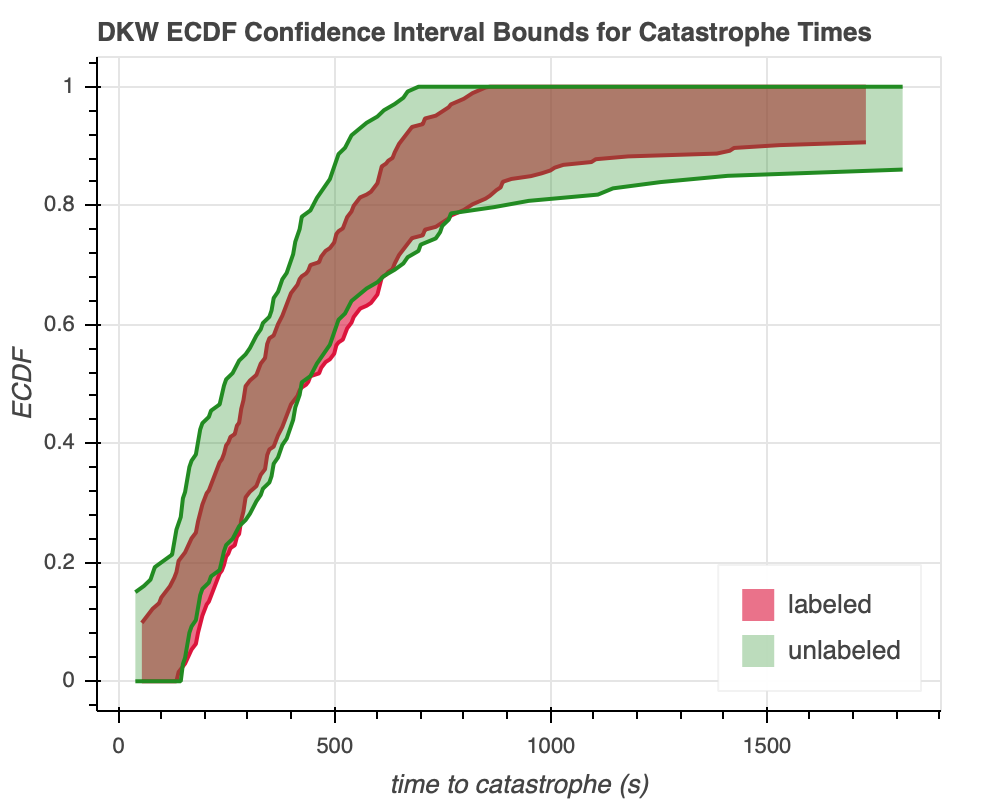
Lastly, we can calculate the lower and upper bounds for the $95$% confidence interval using the DKW equality. The DKW inequality puts an upper bound on the maximum distance between the ECDF $\hat{F}(x)$ and the generative CDF $F(x)$. It states that, for any $\epsilon > 0$,

\begin{align} P \ (\mathrm{sup}_x \ \lvert F(x) - \hat{F}(x) \rvert \ > \epsilon) \ \leq \ 2\mathrm{e}^{2n\epsilon^2}, \end{align}

where $n$ is the number of points in the data set. For a $100 \times (1 - \alpha)$ percent confidence interval, we specify that

\begin{align} \alpha = 2\mathrm{e}^{-2n\epsilon^2}, \end{align}

which gives

\begin{align} \epsilon = \sqrt{\frac{1}{2n} \ \mathrm{log} \ \frac{2}{a}} \end{align}

Then, the lower and upper bounds are:

\begin{align} L(x) = \max\left(0, \hat{F}(x) - \epsilon\right), \end{align}

and the upper bound is

\begin{align} U(x) = \min\left(1, \hat{F}(x) + \epsilon\right). \end{align}

We implement this in viz_controls.py module, and we get Figure 1b.

Figure 1b script dataset

The bounds for the confidence interval of the labeled tubulin generally lie within the bounds for that of the unlabeled type, similar to the confidence intervals themselves. Thus, most of the labeled tubulin looks like it could be behaving like the unlabeled tubulin. However, it's still a possibility that the labeled tubulin acts somewhat differently. This isn't all that unusual––after all, changing environmental conditions means that it can't stay exactly the same. That said, given that catastrophe times can already be up to nearly $2000$ seconds, the differences we observe don't seem so major that they would invalidate the other results in the study.

With all this analysis, we can say that there is no significant difference in the distributions of the labeled and unlabeled tubulin, and we may comfortably use the labeled tubulin as a proxy for the unlabeled tubulin when calculating catastrophe times.