Theory
Gardner et al. assumed that the microtubule catatrophe times are gamma distributed. The gamma distribution models the time we have to wait for $\alpha$ arrivals of a Poisson process, where each subprocess occurs at the same rate $\beta$. As Justin says, "chemical processes are often modeled as Poisson processes, and one can imagine that it may take several successive chemical processes to trigger a catastrophe event. If these processes all have similar rates, the time to catastrophe could be approximately Gamma distributed" (quoted from solutions). Interestingly, even though arrivals are often thought of as integer values, the gamma distribution is continuous and can take on any positive real number. As such, there may be something like $\alpha = 2.4$ arrivals, and the average catastrophe time would be $\frac{\alpha}{\beta}$. The gamma model is well defined, and models of it can be found on Justin's Distribution Explorer.
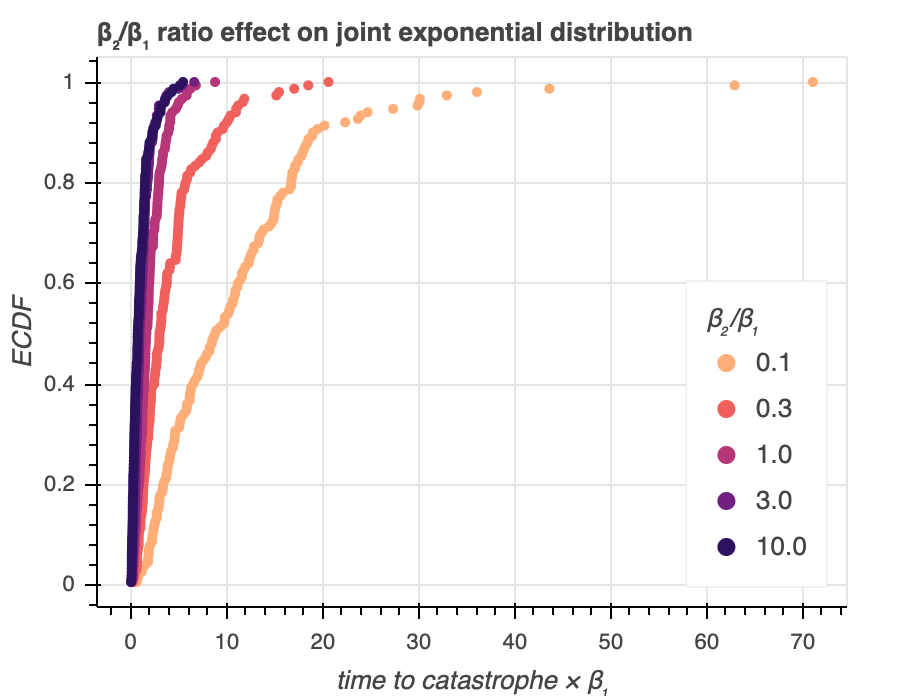
As an alternate model, we propose "that exactly two biochemical processes have to happen in succession to trigger catastrophe. That is, the first process happens, and only after the first process happens can the second one happen. We model each of the two process as a Poisson process. The rate of arrivals for the first one is $\beta_1$ and the rate of arrivals for the second one is $\beta_2$" (quoted from homework problem). In other words, the time to each individual arrival is exponentially distributed, and the sum of the two arrival times is the catastrophe time. We can explore how this idea visually by randomly generating points out of the joint exponential distribution and varying our $\beta_1$ and $\beta_2$ parameter values. We use the viz_explore_two_arrival_story.py module to generate Figure 2a.
We see that when $\beta_2$ is much larger than $\beta_1$, the catastrophe times are much shorter, since having a high rate of arrival for the second event makes the first event the 'limiting step' of the story, and catastrophe can happen very soon after the first event has arrived. On the other hand, when $\beta_2$ is much smaller than $\beta_1$, the catastrophe times are longer, reflecting the fact that the second event takes a while, and it can only happen after the first event has arrived. Of interest, especially in the smaller values of catastrophe times, the distributions all have inflection points. This is different from exponential distributions, which do not.
Deriving the PDF¶
Now, we can get more theoretical and actually calculate the catastrophe time distribution analytically. We will show that the PDF of the distribution matching this story is:
\begin{align} f(t;\beta_1, \beta_2) = \frac{\beta_1 \beta_2}{\beta_2 - \beta_1}\left(\mathrm{e}^{-\beta_1 t} - \mathrm{e}^{-\beta_2 t}\right) \end{align}for $\beta_1 \ne \beta_2$.
Since there are two events that need to happen, we can think of the total time $t$ until catastrophe as the sum of two times––the time to event $1$, plus the time to event $2$. Mathematically, we let $t_1 = \textrm{time to first event}$; $t_2 = \textrm{time to second event, after the first event has happened}$. Then, we say that $t = t_1 + t_2$. Since both the first arrival and the second arrival are individually Poisson distributed, the time between events must be exponentially distributed. As such, we model the probability density functions of $t_1$ and $t_2$ as follows: $f(t_1) = \beta_1 \mathrm{e}^{(-\beta_1 t_1)}$ and $f(t_2) = \beta_2 \mathrm{e}^{(-\beta_2 t_2)}$.
Now, we write the joint distribution of $t_1$ and $t_2$ by multiplying $f(t_1)$ and $f(t_2)$.
\begin{align} f(t_1,t_2) = f(t_1)f(t_2) = \beta_1 \beta_2 \mathrm{e}^{-\beta_1 t_1}\mathrm{e}^{-\beta_2 t_2} \end{align}We also come up with a game-plan to the proof; we first change the variable $t_2$ to $t$ using the equation $t = t_1 + t_2$, and then we marginalize out $t_1$ by summing over all $t_1$ (we actually use an integral, rather than summation, since the time values are continuous). This gives us a distribution for $t$, dependent on $\beta_1$ and $\beta_2$.
\begin{align} f(t_1, t_2) \,\,\, \overrightarrow{change \ of \ var.} \,\,\, f(t_1, t) \,\,\, \overrightarrow{marginalization} \,\,\, f(t) \end{align}So, \begin{align} \\ f(t_1, t_2) = \beta_1 \, \beta_2 \, \mathrm{e}^{-\beta_1 t_1} \, \mathrm{e}^{-\beta_2 t_2} \end{align}
The derivative of $t_2$ with respect to $t$ is $1$, so the Jacobian is just $1$.
\begin{align} f(t_1, t) = \beta_1 \, \beta_2 \, \mathrm{e}^{-\beta_1 t_1} \, \mathrm{e}^{-\beta_2 (t - t_1)} \\ \end{align}Before we marginalize on our problem, this is what marginalization in general looks like: \begin{align} f(t) = \int d t_1 \,\, f(t_1, t) \\ \end{align}
Specifically for us, we will integrate from $0$ to $t$, since $0 \le t_1 \le t$.
\begin{align} f(t) = \int_0^t d t_1 \, \beta_1 \, \beta_2 \, \mathrm{e}^{-\beta_1 t_1} \, \mathrm{e}^{-\beta_2 (t_2 - t_1)} \\ \end{align}From here on out, we are just simplifying. We start by taking out terms that are not $t_1$. Note that we are able to take out an expression with $t$ even though $t = t_1 + t_2$ because we have already done a change of variable and $t_2$ is irrelevant to us now.
\begin{align} f(t) = \beta_1 \, \beta_2 \, \mathrm{e}^{-\beta_2 t} \, \int_0^t d t_1 \, \mathrm{e}^{t_1 (\beta_2 - \beta_1)} \\[1em] f(t) = \beta_1 \, \beta_2 \, \mathrm{e}^{-\beta_2 t} \left[\dfrac{1}{\beta_2 - \beta_1} \, \mathrm{e}^{t_1 (\beta_2 \beta_1 )}\right]_0^t \\[1em] f(t) = \dfrac {\beta_1 \, \beta_2}{\beta_2 - \beta_1} \mathrm{e}^{-\beta_2 t} \left(\mathrm{e}^{t (\beta_2 - \beta_1)} - 1\right) \\[1em] f(t) = \dfrac{\beta_1 \, \beta_2}{\beta_2 - \beta_1} \left( \mathrm{e}^{-\beta_1 t} - \mathrm{e}^{-\beta_2 t} \right) \end{align}and we have shown that the above quantity is the PDF of our story. With this, the CDF of the distribution is:
\begin{align} F(t; \beta_1, \beta_2) = \frac{\beta_1 \beta_2}{\beta_2-\beta_1}\left[ \frac{1}{\beta_1}\left(1-\mathrm{e}^{- \beta_1 t}\right)- \frac{1}{\beta_2}\left(1-\mathrm{e}^{-\beta_2 t}\right) \right]. \end{align}We will be overlaying CDFs over the ECDFs in the next section, but it is good to keep this in our back pocket for now. Now, let's delve even further into this model and derive maximum likelihood estimates for our two parameters, $\beta_1$ and $\beta_2$, both analytically and numerically.
Deriving the MLE Numerically¶
Let's begin by finding the log likelihoood of our PDF. Let's first impose that $\beta_1 \le \beta_2$, which we can do without loss of generality. Now, we can reparametrize by setting $\Delta\beta = \beta_2 - \beta_1 \ge 0$. Let's rewrite PDF as a joint likelihood function:
\begin{align} L(\beta_1, \Delta\beta ; \mathbf{t}) = \prod_{i = 1} ^ {n} \frac{\beta_1 \cdot (\beta_1 + \Delta\beta)}{\Delta\beta}\left(\mathrm{e}^{-\beta_1 t} - \mathrm{e}^{-\beta_1 - \Delta\beta t}\right) \end{align}We assume that $\Delta\beta$ is very small. Unfortunately, that means that the term $\left(\mathrm{e}^{-\beta_1 t} - \mathrm{e}^{-\beta_1 + \Delta\beta t}\right)$ will become very close to zero, and we would prefer not to multiply very small numbers in succession. Instead, we will factor out ${e}^{-\beta_1 t}$ to get:
\begin{align} L(\beta_1, \Delta\beta ; \mathbf{t}) = \prod_{i = 1} ^ {n} \frac{\beta_1 \cdot (\beta_1 + \Delta\beta)}{\Delta\beta} \mathrm{e}^{-\beta_1 t} \left(1 - \mathrm{e}^{-\Delta\beta t}\right) \end{align}Incidentally, this is the first step to the log-sum-exp trick, and we can now take the logs on both sides to get the log-likelihood. Since $\beta_1$ and $\Delta\beta$ are not changing within the summation, they can be summed over $n$ times, and all we need to do is multiply by $n$.
\begin{align} l(\beta_1, \Delta\beta ; \mathbf{t}) & = \sum_{i = 1} ^ {n} \ln \left[ \frac{\beta_1 \cdot (\beta_1 + \Delta\beta)}{\Delta\beta} \mathrm{e}^{-\beta_1 t} \left(1 - \mathrm{e}^{-\Delta\beta t}\right) \right] \\[1em] l(\beta_1, \Delta\beta ; \mathbf{t}) &= n \ln \beta_1 + n \ln(\beta_1 + \Delta\beta) - n \ln( \Delta\beta) - \sum_{i = 1}^{n} \beta_1 t_i + \ln \left(1 - \mathrm{e}^{-\Delta\beta t}\right) \end{align}For now, let's keep this log likelihood function in our back pocket, since we'll need to use it very soon. However, let's first delve deeper into what to do when $\Delta\beta$ approaches $0$. This is clearly an issue, since the rightmost term of our log-likelihood is not well defined at $\Delta\beta = 0$, since $\ln(1 - 1)$ doesn't exist. Luckily, if $\Delta\beta = 0$ or approaches $0$, then our story actually changes into that of the gamma distribution story––$\alpha$ would be $2$, and we would be able to model our two events with the same arrival rate $\beta$. This makes sense intuitively, but we can also do a sanity check with the math. We can write $\Delta\beta$ in terms of $\beta_1$ that satisfies the MLE condition where $\frac{\partial l}{\partial \Delta\beta} = 0$ and $\frac{\partial l}{\partial \beta_1} = 0$. Finding these partial derivatives, we get:
\begin{align} \frac{\partial l}{\partial \Delta\beta} &= \frac{n}{\beta_1 + \Delta\beta} - \frac{n}{\Delta\beta} + \sum^n_{i=1} \frac{t_i \mathrm{e}^{-\Delta\beta t_{i}}}{1 - \mathrm{e}^{-\Delta\beta t_{i}}} \\[1em] \frac{\partial l}{\partial \beta_1} &= \frac{n}{\beta_1} + \frac{n}{\beta_1 + \Delta\beta} - \sum^n_{i=1} t_i \end{align}Taking the second partial derivative and setting it to $0$, we get:
\begin{align} n \beta_1 + n \Delta\beta + n \beta_1 &= \bar{t} n (\beta_1^2 + \beta_1 \Delta\beta) \\[1em] \Delta \beta = \frac{\beta_1(\bar{t} \beta_1 - 2)}{1 - \bar{t} \beta_1} \end{align}Previously, we've enforced that $\Delta\beta \ge 0$, so for non-edge cases, where $\Delta\beta \ne 0$, both the numerator and denominator on the RHS must have the same signs. In other words, we have two cases:
Case 1 \begin{align} &\bar{t} \beta_1 - 2 > 0 \ \wedge \ 1 - \bar{t} \beta_1 > 0 \\[1em] &\bar{t} \beta_1 > 2 \ \wedge \ \bar{t} \beta_1 < 1 \end{align}
Case 2 \begin{align} &\bar{t} \beta_1 - 2 < 0 \ \wedge \ 1 - \bar{t} \beta_1 < 0 \\[1em] &\bar{t} \beta_1 < 2 \ \wedge \ \bar{t} \beta_1 > 1 \end{align}
Scenario 1 is impossible, so we have scenario 2 where $1 < \bar{t} \beta_1 < 2$. Now, in the edge case where $\Delta\beta = 0$, what happens? We know from $\Delta \beta = \frac{\beta_1(\bar{t} \beta_1 - 2)}{1 - \bar{t} \beta_1}$ that when $\Delta\beta = 0$, either $\beta_1 = 0$ or $\bar{t} \beta_1 - 2 = 0$. We can figure this out by looking at the derivative of $\Delta\beta$ with respect to $\beta_1$.
\begin{align} \frac{d \Delta\beta}{d \beta_1} &= \frac{(2 \beta_1 \bar{t} - 2)(1 - \bar{t} \beta_1) + \bar{t}(\beta_1^2 \bar{t} - 2 \beta_1)}{(1 - \bar{t} \beta_1)^2} \\[1em] \frac{d \Delta\beta}{d \beta_1} &= -\frac{2 \beta \bar{t} - 2 \beta_1^2 \bar{t}^2 - 2 + 2 \bar{t} \beta_1 + \bar{t}^2 \beta_1^2 - 2 \bar{t} \beta_1}{(1 - \bar{t} \beta_1)^2} \\[1em] \frac{d \Delta\beta}{d \beta_1} &= -\frac{1 + (\beta_1 \bar{t} - 1)^2}{(\beta_1 \bar{t} - 1)^2} \end{align}From our resulting expression for the derivative, we see that $\frac{d \Delta\beta}{d \beta_1}$ is always negative, and that $\Delta\beta$ is monotonically decreasing over $\beta_1$. All this is to say that as $\beta_1$ approaches its maximum, which we previously showed to be $\frac{2}{\bar{t}}$, $\Delta\beta$ will reach its minimum. Since the minimum that $\Delta\beta$ can approach is $0$, as $\Delta\beta \rightarrow 0$, $\bar{t}\beta_1 - 2 \rightarrow 0$. In other words, we know that $\beta_1 \not\rightarrow 0$, but rather $\beta_1 \rightarrow \frac{2}{\bar{t}}$ when $\Delta\beta \rightarrow 0$. This gives us some mathematical backing behind how the two-event story collapses into a gamma distribution with $\alpha = 2$ when $beta_1$ and $beta_2$ are very close to each other. We use this information in our mle function that we write in parameter_estimates.py. There, we use Powell's method for optimization and add a tolerance of $1e-8$ to make our values more consistent from run to run.
Now, we still have to set our initial guesses for our parameter estimates. We've seen before how important these estimates are, and so let's come up with some good estimates. We've already seen that
\begin{align} \Delta \beta = \frac{\beta_1(\bar{t} \beta_1 - 2)}{1 - \bar{t} \beta_1} \end{align}We can substitute this into \begin{align} \frac{\partial l}{\partial \Delta\beta} &= \frac{n}{\beta_1 + \Delta\beta} - \frac{n}{\Delta\beta} + \sum^n_{i=1} \frac{t_i \mathrm{e}^{-\Delta\beta t_{i}}}{1 - \mathrm{e}^{-\Delta\beta t_{i}}} \end{align}
to get an expression:
\begin{align} \Delta \beta = \frac{\beta_1(\bar{t} \beta_1 - 2)}{1 - \bar{t} \beta_1} \end{align}We can substitute this into \begin{align} \frac{\partial l}{\partial \Delta\beta} &= \frac{n}{\beta_1 + \frac{\beta_1(\bar{t} \beta_1 - 2)}{1 - \bar{t} \beta_1}} - \frac{n}{\frac{\beta_1(\bar{t} \beta_1 - 2)}{1 - \bar{t} \beta_1}} + \sum^n_{i=1} \frac{t_i \mathrm{e}^{-\frac{\beta_1(\bar{t} \beta_1 - 2)}{1 - \bar{t} \beta_1} t_{i}}}{1 - \mathrm{e}^{-\frac{\beta_1(\bar{t} \beta_1 - 2)}{1 - \bar{t} \beta_1} t_{i}}} \end{align}
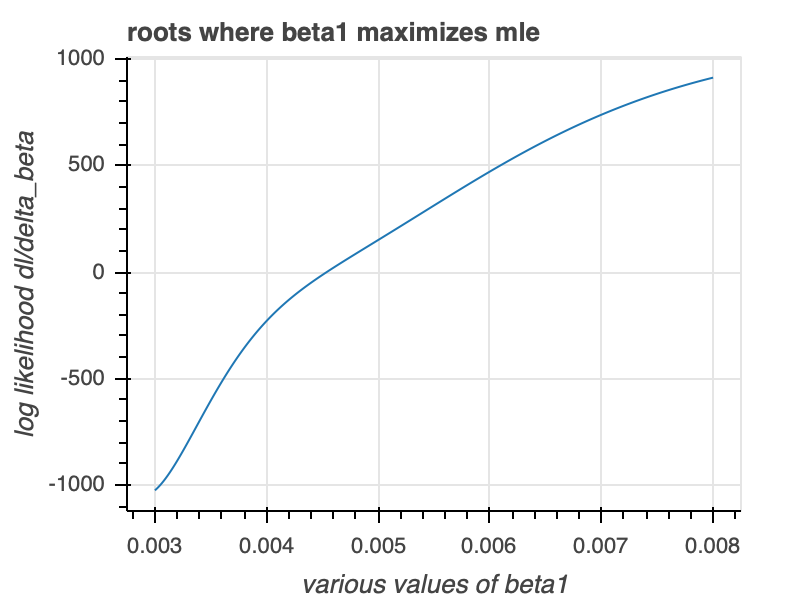
This doesn't look too great, but we are only using it to get an estimate. For the MLE, this quantity would be set to $0$, and we would essentially be doing root-finding to find what values of $\beta$ make the expression equal to $0$. We can code the function up, plot it, and use scipy.optimize.brentq to find the roots. Plotting this equation using viz_explore_two_arrival_story.py, we get Figure 2b.
We see the graph pass through $0$, which is good news. We can now find the roots, knowing that it is somewhere between $(0.003, 0.008)$. This is also done in viz_explore_two_arrival_story.py, and we get the brentq root to be $0.004538126244018046$. Incidentally, this value is extremely close to $\frac{2}{\bar{t}}$ ($0.004538122378750404$), which we previously saw is the maximum value for $\beta_1$. Since we may need to do this estimation multiple times in the future, we will simply approximate $beta_1$ as $\frac{2}{\bar{t}}$, and we approximate $\Delta\beta$ to be a very small (but not zero, since that will give us some issues with parameter estimates) number.
After implementing all of this theory, we draw MLEs for $\beta$ and $\Delta \beta$ and get that $\beta_1$'s MLE is $0.0045381223 \ s^{-1}$, while $\Delta \beta$'s is $0.0000000062$. Interestingly, we get values of $\Delta\beta$ that are basically negligible, meaning that $\beta_1$ and $\beta_2$ are similar. In other words, the two arrivals are most likely to have similar rates, given our data. We can also find the MLE estimate for $\beta_2$, which we'll need for confidence interval plotting later, and we get that $\beta_2$'s MLE is $0.0045381285 \ s^{-1}$. As we mentioned earlier, $\beta_1$ and $\beta_2$ are very similar, and we can actually show this analytically as well, which we do now.
Deriving the MLE Analytically¶
Previously, we've already seen that when $\Delta \beta = 0$, we have that $\beta_1 = 2/\bar{t}$. To maximize the likelihood for $\Delta \beta$, we need to find the value of $\Delta\beta$ that results in $\partial \ell /\partial \Delta\beta = 0$. We assume that $\Delta\beta$ is small and then show that $\Delta\beta = 0$ indeed is the MLE satisfying $\partial \ell /\partial \Delta\beta = 0$. For small $\Delta \beta$, we Taylor-expand to get:
\begin{align} \frac{\mathrm{e}^{-\Delta\beta t_i}}{1 - \mathrm{e}^{-\Delta\beta t_i}} \approx \frac{1}{\Delta \beta t_i} - \frac{1}{2}. \end{align}Inserting this expression into our expression for $\partial\ell/\partial \Delta\beta$ gives
\begin{align} \frac{\partial \ell}{\partial \Delta\beta} &= -\frac{n}{\Delta\beta} + \frac{n}{\beta_1 + \Delta\beta} +\sum_{i=1}^n\left(\frac{1}{\Delta\beta}-\frac{t_i}{2}\right) \\[1em] &= -\frac{n}{\Delta\beta} + \frac{n}{\beta_1 + \Delta\beta} + \frac{n}{\Delta\beta} -\frac{n\bar{t}}{2} \\[1em] &= \frac{n}{\beta_1 + \Delta\beta} - \frac{n\bar{t}}{2}. \end{align}When this expression equals zero, we have our MLE. Choosing $\Delta\beta = 0$, and therefore that $\beta_1 = 2/\bar{t}$, satisfies $\partial \ell/\partial\Delta\beta = 0$. Therefore, the MLE is $\beta_1 = 2/\bar{t}$ and $\Delta\beta = 0$, or equivalently, $\beta_1 = \beta_2 = 2/\bar{t}$. Essentially, our MLEs suggest that the two-story model collapses down to the gamma distribution with $\alpha = 2$ when the arrival rates are similar (note: this last section, from 'previously, we've seen...' was copied from the solutions and lightly modified).
Now, we are done with the theory parts, and we're set to plot some confidence intervals/regions of our parameters for both our gamma distribution story and two-event story. The parameters for the gamma distribution are $\alpha$ and $\beta$, while the parameters for the two-event story are $\beta_1$ and $\Delta \beta$, or more preferably, $\beta_1$ and $\beta_2$. Here, we use the viz_parameter_estimates.py module to generate all the plots of Figure 3.
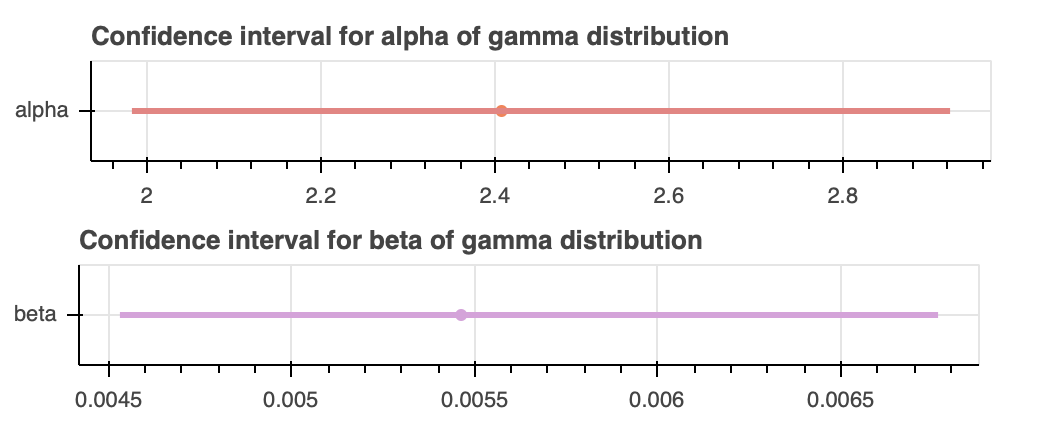
Plots¶
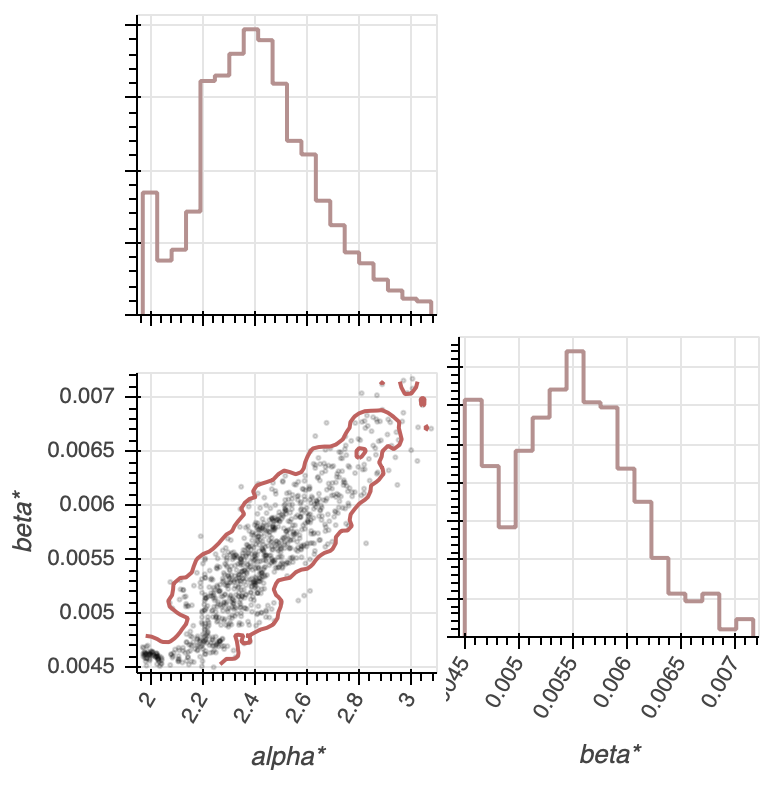
As an initial guess for the gamma distribution $\alpha$, we estimate that there will be around $2$ arrivals. We choose $2$ mostly because we will later be modeling based on a two biochemical process story. In addition, chemically, it might be difficult to require a large number of arrivals to occur before catastrophe, since each successive arrival would make the overall chance for getting catastrophe lower and lower; and, as we've seen in previous problems, catastrophe is not a particularly rare event. As seen in the confidence intervals, the gamma distribution suggests that there are around $2.4$ arrivals, with a $95$% confidence interval of $[1.98242, 2.91772]$. Chemically, it sounds something funky may be going on. Perhaps there are two different populations of the microtubules, and there might be some mixture modeling going on, thus giving us a non-integer $\alpha$. Or, maybe dimerization may affect the number of average arrivals, if one arrival might affect multiple microtubules. There may be other better explanations as well. The $\beta$ is $0.00546287$ and represents the arrival rate, which suggests that it takes approximately $183$ seconds for one arrival to come.While the confidence interval plots look nice, since we have two parameters, it would more informative to look at a corner plot, since that way we can tell how different values of $\alpha$ and $\beta$ vary with each other, and what values of $\alpha$ and $\beta$ pairs are within the $95$% confidence interval. We see this in Figure 3b.
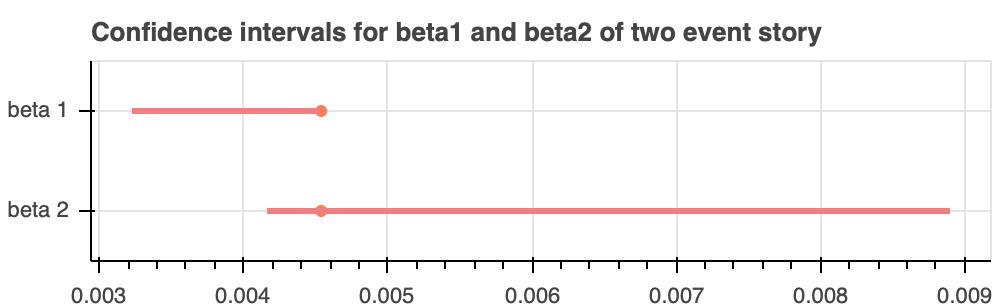
Not surprisingly, we see that $\alpha$ and $\beta$ are positively correlated; this makes sense because the more arrivals there are, the faster each arrival would have to come within the catastrophe timeframe; thus, we cannot have a large $\alpha$ with a small $\beta$. Interestingly for the $95$% confidence region, values of $\alpha$ generally fall between $2$ and $3$, while $\beta$ falls between $0.0045$ and $0.007$. This suggests that there are between $2$ and $3$ arrivals. Now, we plot the confidence intervals for the two story distribution parameters, as seen in Figure 3c.
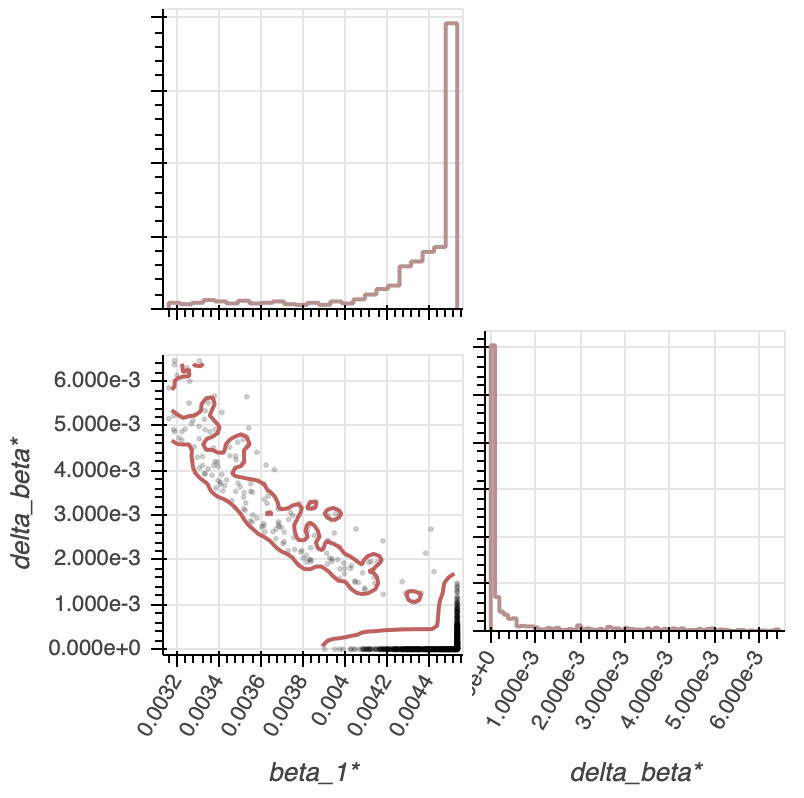
The confidence interval for $\beta_1$ is $[0.003261, 0.004538]$, while $\beta_2$'s is $[0.004147, 0.008550]$. We mentioned previously that $\beta_1$'s MLE is $0.0045381223$, while $\beta_2$'s MLE is $0.0045381285$, both in inverse seconds. This is interesting, because our MLE essentially collapses down to a gamma distribution with $\alpha = 2$. In other words, given our set of catastrophe times, it is difficult to wheedle out what portion of the time is before to the arrival of the first event, and what portion of the time is between the first and second event. It also makes sense that the confidence intervals show $\beta_2$ as being greater in value than $\beta_1$, since we originally enforced that $\beta_2 \ge \beta_1$. Nevertheless, it is interesting to see that the MLEs still have them finding each other at the same values. Let's also make a corner plot between $\beta_1$ and $\Delta \beta$ to see how $\beta_1$ and $\Delta \beta$ are correlated, as seen in Figure 3d.
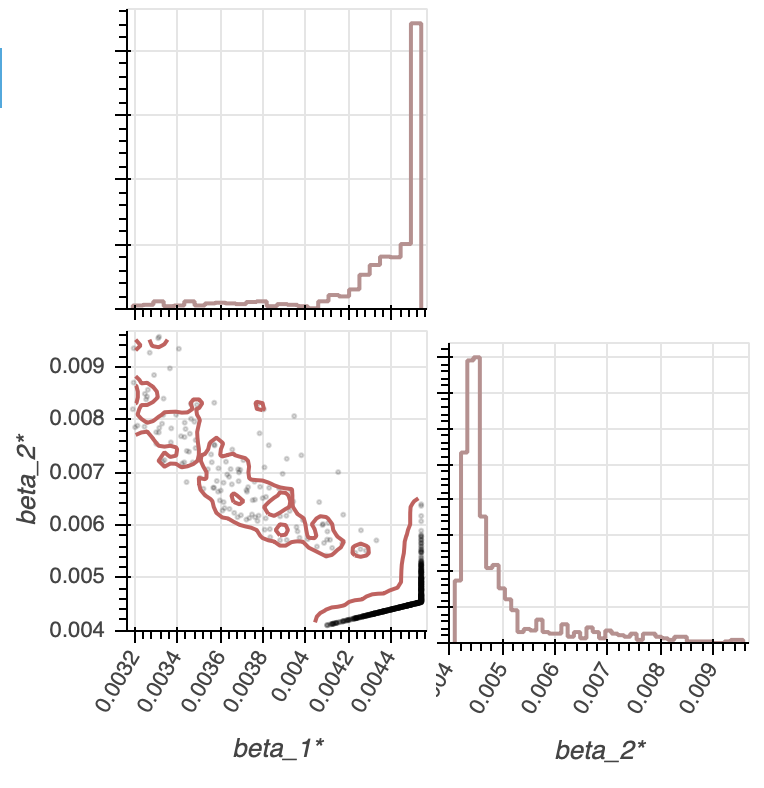
There is a negative correlation between $\Delta \beta$ and $\beta_1$, as expected from our mathematical insight of $\Delta \beta$ being monotonically decreasing over $\beta_1$. For a given $\beta_1$, the allowed values, within a $95$% confidence interval, for $\Delta \beta$ are pretty small, since we need $\beta_2$ to have a certain arrival rate in order to match the catastrophe times in our data. We can also plot a corner plot for $\beta_1$ and $\beta_2$ to compare the two, as seen in Figure 3e.
Here, it is actually more difficult to see that the MLEs for $\beta_1$ and $\beta_2$ are nearly identical, since the $95$% confidence intervals show a large range of $\beta_1$ and $\beta_2$'s. Nevertheless, we still see that as $\beta_2$ decreases, $\beta_1$ increases, which makes sense given that the total time for arrival was optimized to match that of the emperical catastrophe times. Now, we've done enough theoretical parameter estimates type analysis, and we are ready to graduate to model comparison in the next section.